2024 KAKAO WINTER INTERNSHIP 문제
도넛 모양 그래프, 막대 모양 그래프, 8자 모양 그래프들이 있습니다. 이 그래프들은 1개 이상의 정점과, 정점들을 연결하는 단방향 간선으로 이루어져 있습니다...
그래프 용어를 오랜만에 보아서 조금 당황했었다

크기가 n 인 세가지 종류 그래프들이 있을 수 있고 각각 특징이 있다.
어떤 크기, 어떤 종류의 그래프가 있을지 모르고 각 그래프 정점마다 서로 다른 번호가 매겨지며
생성되는 그래프 수의 합은 2 이상!
이때, 새로운 번호가 매겨진 새 정점 하나가 추가 된다.
이 정점은 다른 그래프들의 임의의 정점 하나로 향해 연결되는 간선이 만들어진다!
간선 정보를 담은 2차원 배열이 주어지고, 이 정보로 어떤 그래프가 몇개 있는지, 새로 생긴 정점은 몇 번 인지 알아내라!
하는 문제이다!
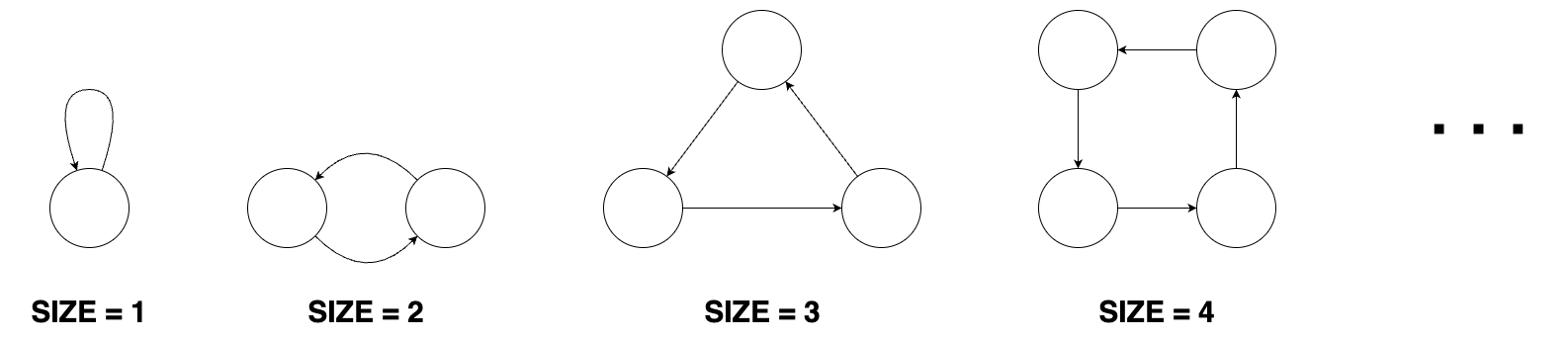
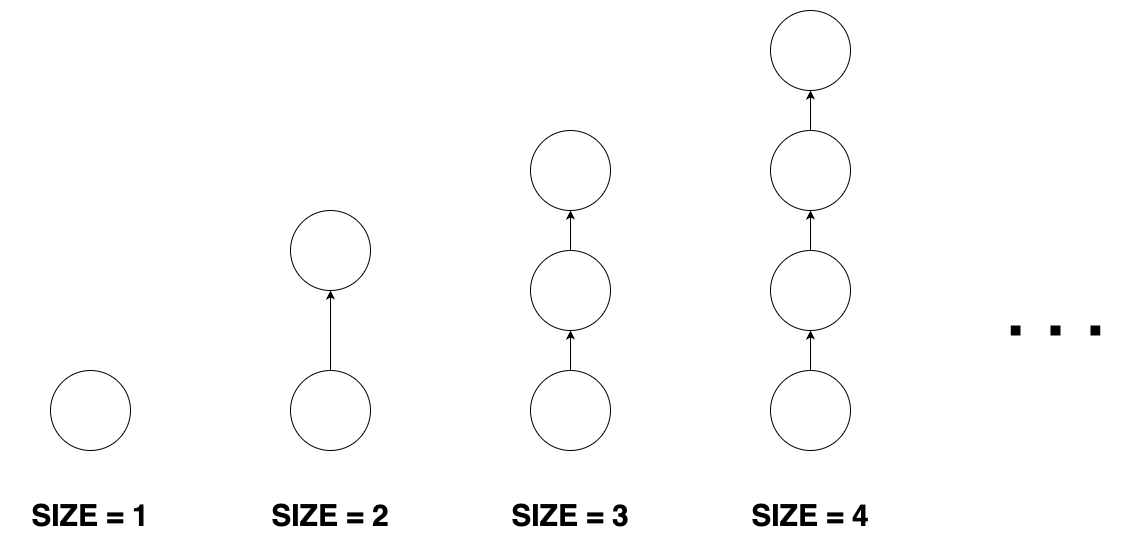
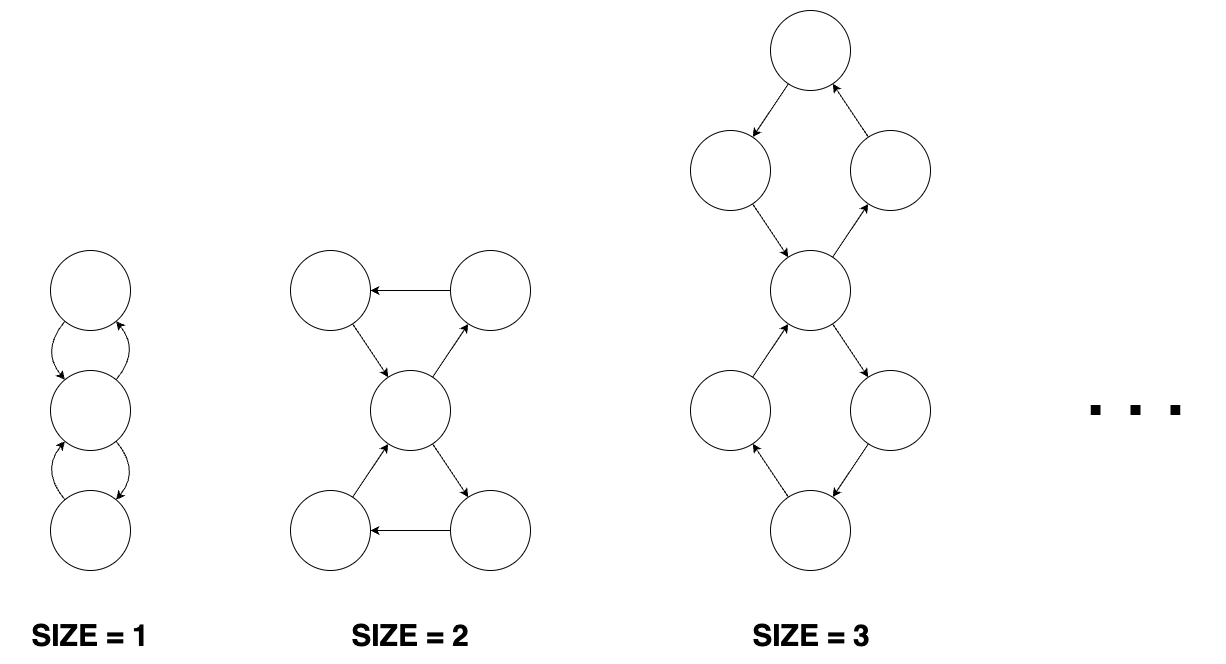
그림으로 보면 이렇게 생겼다!
간선 정보만 가지고 그래프의 수를 알아내려면 각 그래프가 가진 간선의 특징을 알아봐야 할 것 같았다..
1. 도넛 모양 그래프
size=1 일때는 하나의 간선이 하나의 정점을 돌고, 나머지는 들어오는 간선과 나가는 간선이 1개씩
size=1 일때를 제외하고는 모든 정점이 같은 특징을 보이므로 몇 개의 그래프로 나뉜 것인지 알아내기 어렵다
전체 그래프 수 에서 막대와 8자 그래프 수를 빼주면 나올 것!
2. 막대 모양 그래프
size=1 일때는 들어오는 간선 0개, 나가는 간선 0개, 나머지의 경우는 맨 마지막 정점이 들어오는 간선 1개. 나가는 간선 1개 ( 들어오는, 나가는 너무 기니까 [in,out] 으로 대체하겠다 )
새 정점이 막대 모양 그래프의 임의의 정점에 연결 된다면! size=1 일때는 [1,0], 나머지의 경우 맨 마지막 정점은 [2,0] 으로 하나의 그래프당 무조건 [1이상,0] 의 정점이 생기는 특징!
3. 8자 모양 그래프
그래프 1개가 있다면 중간 정점이 무조건 있고 간선은 [2,2] 이다
새 정점에서 임의로 연결되면 중간에 연결 된다면 [3,2] 아니라면 [2,2] 이므로 무조건 [2이상,2] 의 정점이 생기는 특징!
4. 새로운 정점
그래프 총 합이 무조건 2개 이상 이고, 새로 생긴 정점에는 아무 간선도 들어오지 않으므로
간선 특징은 [0,2이상] 이 된다!
자.. 이걸 정리해서 최종 코드는 이렇다!
def solution(edges):
nlist=[]
for ed in edges:
nlist.append(ed[0])
nlist.append(ed[1])
nlist = list(set(nlist)) # 정점들을 유니크하게 보기 위함
node_dict={}
for n in nlist:
node_dict[n]=[0,0] # in,out
# 정점마다 in,out 체크
for ed in edges:
node_dict[ed[0]][1]+=1
node_dict[ed[1]][0]+=1
answer=[0,0,0,0]
for n,info in node_dict.items():
if info[0]==0 and info[1]>=2: # 새 정점
answer[0]=n
elif info[0]>=1 and info[1]==0: # 막대
answer[2]+=1
elif info[0]>=2 and info[1]==2: # 8자
answer[3]+=1
total=0
for ed in edges: # 정점에서 연결 체크
if ed[0]==answer[0]:
total+=1
# 새 정점으로 알아낸 그래프 총 합에서 막대,8자 그래프 수 빼기
answer[1]=(total-answer[2]-answer[3])
return answer
각 그래프마다 특징이 있구나! 하는걸 처음부터 알아차리지 못해서 시간이 조금 걸렸지만 끝~
